
불 대수의 개요
불 대수란 논리식을 알기위한 기본적인 성질을 수학적으로 표현하기 위한 구조이다. 영국의 수학자 G. Boole이 만들었다. 어째서 우리가 논리식을 알아야하는 걸까?임베디드기사를 준비하고 있는 나와 독자들은 디지털 시스템(Digital System)을 마스터 하고자한다. 이 “디지털”은 이산적(Binary; 원문은 Discrete이지만 넘어가자)이고 논리식의 참/거짓의 성질과 1/0을 대응하여 컴퓨터논리의 이해에 그대로 적용할 수 있다. 위키백과에서는 불 대수를 다음과 같이 정의내리고 있다.
순서론과 추상대수학, 논리학에서 불 대수(Boole代數, 영어: Boolean algebra)는 고전 명제 논리의 명제의 격자와 같은 성질을 갖는 격자이다. 즉, 논리적 공리들을 만족시키는 논리합과 논리곱 및 부정의 연산이 정의된 대수 구조이다.
-위키백과 : 불 대수
(https://ko.wikipedia.org/wiki/%EB%B6%88_%EB%8C%80%EC%88%98)
위의 페이지에서도 볼 수 있듯 컴퓨터에서 가지는 높은 전압(H)를 1(혹은 True를 표현하는 T)로, 낮은 전압(L)을 0(혹은 False를 표현하는 F)으로 표현하여 조합 회로의 논리표현에 불 대수가 사용된다.
불 대수의 기본연산
먼저 이야기 해두자면 불 대수에서 표현하는 0과 1은 수치적인 값이 아니다. 참과 거짓을 논하고 있기 때문에 이를 매개변수로 사용하는 수학적인 기호도 논리학에서 사용하는 성질을 따르며 일반수학에서 적용되는 연산이 아니라는 점을 참고바란다.
가장 기본적인 연산은 AND / OR / NOT 이 있다
- AND : AND연산은 기호로 *로 표시한다. 양옆의 두 개 인자가 둘다 참일때만 참(1)을 반환하고 하나라도 거짓이 있으면 거짓(0)을 반환한다.
- OR : OR연산은 기호로 +로 표시한다. 양옆의 두 개 인자가 하나라도 참이면 참(1)을 반환하고 둘다 거짓인 경우에만 거짓(0)을 반환한다.
- NOT : NOT은 뒤에 있는 인자가 참이면 거짓을, 거짓참을 반환하는 연산이다. 2진 체계에서 1의 보수연산과 같기 때문에 보수를 의미하는 Complementation으로 표기하기도 한다.
어떠한 논리식에 대해 가질 수 있는 모든 변수에 결과로 대응한 표를 진리표라고 칭한다. 다음은 가장 기본연산인 AND / OR / NOT의 진리표와 회로기호로의 표현이다.
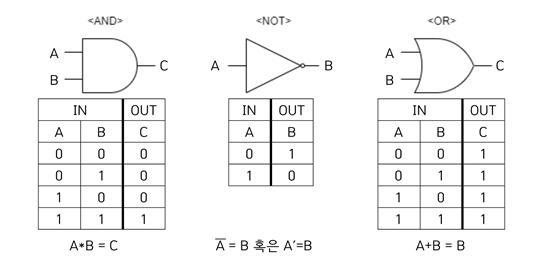
위의 논리표에서 볼 수 있듯이 불 대수에서 사용되는 임의의 논리 변수는 문자로 표현한다. 반면 항상 참인 값(1)과 거짓인 값(0)을 식에 표현할 때도 있으니 참고 바라며,(EX : A*1 = B+0 etc) 아래의 기본정리를 알기 위해서 위의 수식은 자연스럽게 사용할 수 있도록 해두는 것이 좋다.
AND / OR 는 연산 최종결과에 NOT이 붙은 것을 줄여 NAND / NOR로 부르기도 한다. 회로기호결과값에 동그라미 가 붙는 것으로 표현된다,
참고로 1과 1의 덧샘값이 1이 되는 이유는 앞서 설명하였듯 이것이 논리의 분야이기 때문이다. 참/거짓 혹은 이진수로 0/1표현되는 이곳에 2는 없다. 이것은 상태(1은 On 0은 Off)를 나타내는 표현이다. 또한 곱하기 기호(*)는 생략하여 표현이 가능하다.
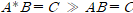
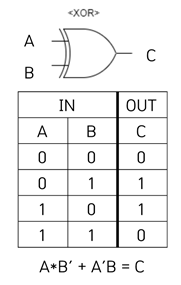
기본연산은 아니지만 논리회로에 자주 사용되는 연산으로 XOR 연산이 있다. 배타적 합 연산 이라고 칭하며, 피연산자 A와 B의 값이 다르면 1, 같으면 0으로 표현된다.
불 대수의 기본정리
불 대수에는 공리처럼 여겨지는 기본 정리가 존재한다. 순수수학 대수체계에 존재하는 그것들(우리가 고등학교 수학에서 배우는 그 정리들)과 매우 유사하다. 이러한 정리를 활용하여 불대수의 논리적 결과를 유지한 상태로 불 대수 식을 변형할 수 있다.
동일 법칙(Identity Laws)
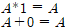
임의의 값 A에 항상 참(1)인 값을 곱하면 그 값은 항상 값 A와 같다. 또한 임의의 값 A에 항상 거짓(0)인 값을 더하면 그 값은 항상 값 A와 같다. (A가 1일 때 0일 때를 각각 가정해 보기를 바란다. 변수가 복잡해져도 그것을 A로 치환한다고 생각한다면 항상 맞는 법칙이 된다.)
지배 법칙(Domination Laws)
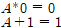
동일 법칙과 반대되는 성질로 임의의 값 A에 항상 거짓(0)인 값을 곱하면 항상 거짓(0)이 되고 임의의 값 A에 항상 참(1)인 값을 더하면 그 값은 항상 참(1)이 된다.
등멱 법칙(Idempotent Laws)
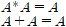
임의의 값 A에 자기 자신을 곱하거나 더해도 A가 된다.(당연 하다 0+0=0, 1+1=1, 0*0=0, 1*1=1)
부정 법칙(Negation Laws)
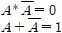
등멱 법칙의 반대되는 법칙으로 임의의 값 A에 자기 자신의 부정(NOT)값을 곱하거나 무조건 거짓(0), 더하면 무조건 참(1)이 된다.
교환 법칙(Commutative Laws)
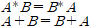
AND나 OR연산에서 피연산자의 위치가 바뀌어도 결과는 동일하다.
결합 법칙(Associative Laws)
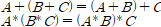
AND나 OR의 연속된 같은 연산이라면 무엇부터 수행하더라도 결과는 동일하다.
분배 법칙(Distributive Laws)
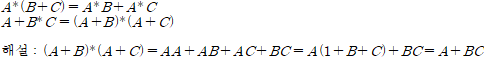
괄호로 먼저계산되는 식을 해체하면 그 수식에 모두 적용되는 연산을 적용된 결과와 같다.
드 모르간의 법칙(De Morgan’s Laws)
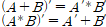
괄호 전체에 부정연산(NOT)연산을 적용하면 각 변수에 NOT연산을 하고 AND연산을 OR로, OR연산을 AND로 변환한다.
이중 부정의 법칙(Dual negation Laws)
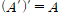
부정을 두 번하면 원래의 값으로 돌아온다. Sim-Ple하다.
흡수 법칙(Absorption Laws)
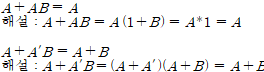
위의 기본 증명들을 활용하여 유도할 수 있는 법칙이다.
정리
불 대수는 디지털 시스템에서 컴퓨터 논리를 표현하기위한 수식이다. 불 대수를 활용하면 복잡한 컴퓨터의 논리를 표현할 수 있다. 불 대수에는 기본연산이 되는 AND / OR / NOT이 존재한다. 또한 불 대수에 적용되는 기본 법칙들이 존재한다.
다음시간에는
다음시간에는 논리식의 간소화를 알아보도록 하겠다.
'자격 > 임베디드기사' 카테고리의 다른 글
| [임베디드기사] [필기] 논리게이트와 조합논리회로(가산기/복호&부호기/선택&분배기) (0) | 2023.08.14 |
|---|---|
| [임베디드기사] [필기] 수의표현(2진수 / 8진수 / 16진수 / 10진수) (0) | 2023.08.13 |
| [임베디드기사] [필기] 논리식의 간소화 (0) | 2023.08.13 |
| [임베디드기사] [필기] 디지털시스템(Digital System) (0) | 2023.08.12 |
| [임베디드기사] 자격에 대하여 (0) | 2023.08.12 |
