
개요
불 대수로 표현된 논리식은 불 대수의 연산법칙을 적용하여 간소화 할 수 있다.
간소화는 회로를 단순하게 만들어주고, 비용을 낮춰주며 이해를 돕기 때문에 어떠한 논리식을 작성한 이후로는 이를 간소화시켜주는 작업이 필요하다. 예를 들면 어떠한 컴퓨터 논리를 작성한 결과가 AB + AB’ 였다면 이는 A(B+B’) 이고 결국 그냥 A와 같은 논리식이 된다. AND연산 2개와 NOT연산 1개, OR연산 1개 있던 것이 그냥 연산이 없어지는 것과 같다. 혹은 아래와 같은 복잡한 연산도 드모르간의 법칙 등을 활용해 간소화 할 수 있다.
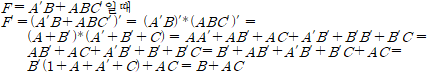
그러나 너무 복잡해 진다면 이런 수학적인 방법(계산과 법칙)을 선택하는 것이 최소한으로 간소화된 식을 얻을 수 있는 최적의 방법이 되진 못한다.(어쩔 수 없지뭐... 사람이 감으로 하는 거니까..)
간소화 방식 – 카르노맵(Karnaugh map)
카르노 맵은 불 대수 함수식을 단순화 하는 방식이다. 요는 논리식을 구성하는 인자들의 구성요소를 최소항 전개(참을 출력하는 인자곱들의 합성으로 이루어진 수식) 하여 도표를 통해 간소화 하는 방식이다. 아래는 예시이다.
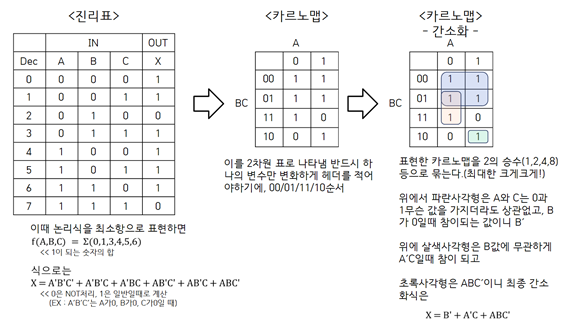
혹시나 시험에 나올 수도 있어서 적어두는 것인데, 최소항을 표현할 때 Don’t Care 인자가 존재할 수 있다.(X)로 표시됨. 이는 간소화 시에 결합해도 되고(사각형 처리) 안해도 상관 없는 항이라는 의미이다.
간소화 방식 - 콰인 매클러스키(Quine-McCluskey Algorithm)
콰인 매클러스키 알고리즘은 주어진 논리식의 후보항을 구하고 한 인자만 변한다면 지배되는 법칙(AB+AB’=A)을 활용하여 논리식을 간소화 하는 방식이다. 기본적으로 노가다 이지만 변수의 개수가 5개 이상이 되는 논리식에서는 카르노 맵이 제한이 생기기 때문에(열 헤더의 생성 난해함, 5개까지는 되긴한다) 콰인 매클러스키 방식을 사용한다.
나중에 시간이 생기면 문제까지 예시로 넣는 것으로 하고 우선 위키백과에 좋은 예시까지 나와있으니 링크를 걸도록 하겠다.
최소항을 찾는 콰인 매클러스키방식을 조금 더 발전 시킨 패트릭 방법이라는 것이 있다. 참고만 하고 있자.
정리
논리식은 같은 논리식으로(동치) 간소화 할 수 있다. 이해도를 증진시키고, 비용을 절감하는 등 여러 가지 장점을 가지고 있는 논리식 간소화는 불 대수의 기본 법칙을 활용한 방식, 카르노 맵을 이용한 방식, 콰인 매클러스키방식이 존재한다.
다음시간에는
다음 시간에는 진수표현 방식에 대해서 알아보도록 하겠다.
'자격 > 임베디드기사' 카테고리의 다른 글
| [임베디드기사] [필기] 논리게이트와 조합논리회로(가산기/복호&부호기/선택&분배기) (0) | 2023.08.14 |
|---|---|
| [임베디드기사] [필기] 수의표현(2진수 / 8진수 / 16진수 / 10진수) (0) | 2023.08.13 |
| [임베디드기사] [필기] 불 대수(Boolean Algebra) (0) | 2023.08.12 |
| [임베디드기사] [필기] 디지털시스템(Digital System) (0) | 2023.08.12 |
| [임베디드기사] 자격에 대하여 (0) | 2023.08.12 |
