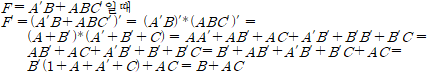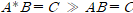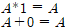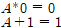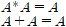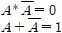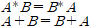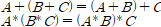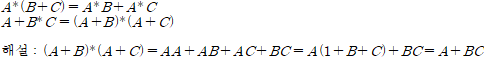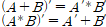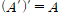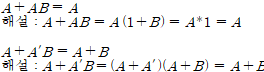논리게이트를 읽고 오기전에 불 대수에 대해서 제대로 알지 못하는 사람들은 필자의 불 대수 포스팅을 읽고 오기를 바란다.
[임베디드기사] [필기] 불 대수(Boolean Algebra)
불 대수의 개요 불 대수란 논리식을 알기위한 기본적인 성질을 수학적으로 표현하기 위한 구조이다. 영국의 수학자 G. Boole이 만들었다. 어째서 우리가 논리식을 알아야하는 걸까?임베디드기사
tutoreducto.tistory.com
논리게이트의 개요
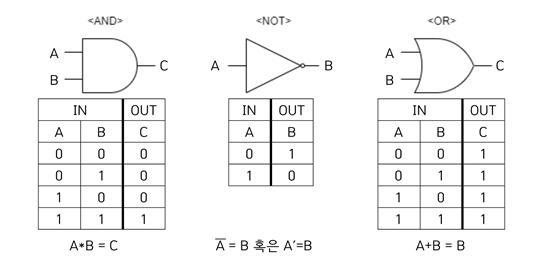
논리게이트는 논리식에서 사용되는 기본연산(AND / OR 등) 회로에 사용하기 위해서 표현하는 도식화된 기호이다. 기호들을 사용해서 회로도면상에 논리식을 표현할 수 있으며 바로 보도록 하자

조합논리 회로
위와 같은 기본 논리게이트를 활용해서 특정한 목적을 수행하는 단위 논리회로를 만들 수 있다. 시험 출제범위로 존재하는 조합논리회로에 대해서 알아보도록 하자. 아래에서 표현되는 모든 회로도는 위키백과에서 참고하였다.
출처 :
* 가산기 : https://ko.wikipedia.org/wiki/%EA%B0%80%EC%82%B0%EA%B8%B0
* 부호기 : https://ko.wikipedia.org/wiki/%EB%B6%80%ED%98%B8%ED%99%94
* 복호기 : https://ko.wikipedia.org/wiki/%EB%B3%B5%ED%98%B8%ED%99%94
* Mux&DeMux : 자체제작
가산기 – 반 가산기(Half Adder)
반 가산기는 이진수의 한자리 수 덧셈을 수행하고 자리올림이 발생하면 Carry 값으로 표현하는 조합논리회로이다.
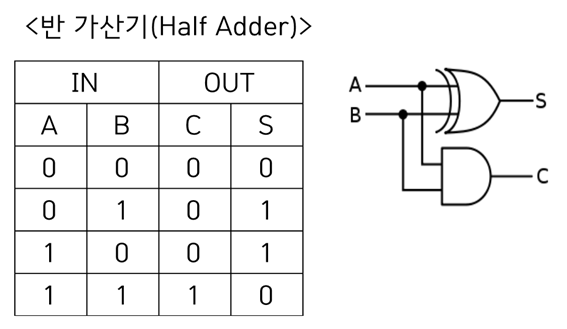
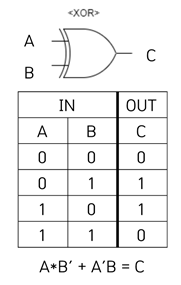
입력으로 A/B가 존재할 때 둘 다 1이거나 0이면 덧셈의 결과는 0이다.(둘다 1일 경우 합의 결과는 0이고 자리올림(S)발생), 한쪽만 1인 경우에만 1이 반환되고 이는 XOR회로와 같다.
반면 자리올림 값은 둘다 1인경우에만 발생하기 때문에 AND게이트로 표현하면 반가산기가 된다. XOR의 진리식이 F=A’B+AB’ 인 것을 생각하면 반가산기는 AND / OR / NOT만으로 구성이 가능한 것이다.
가산기 – 전 가산기(Full Adder)
전 가산기는 반가산기에서 아래 자리에서 발생한 캐리 값이라는 한 가지의 입력을 더 받는다. 단순하게 생각하면 인자가 3개인 덧셈회로와 다르지 않다.
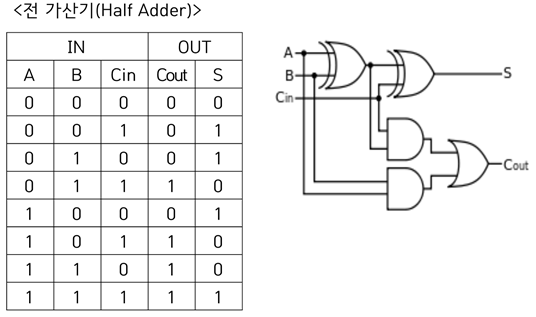
진리표를 통해서 보면 알 수 있듯 이 S는 3개의 합을 나타내고 Cout은 캐리값 발생에 중심을 둔다. 카르노맵을 통해서 해당논리식을 구해보면 S=A⊕B⊕C, Cout=AB+(Cin(A⊕B))가 된다. 이를 회로로 구현하면 반가산기 2개와 OR 게이트 하나가 됨을 알 수 있다.
가산기를 복수개 사용하면 여러자리수를 더하는 논리회로를 만들 수 있다. 이전자리에서 발생한 Carry out 비트를 다음 전가산기의 Cin으로 사용하는 방식인데, 자리올림수가 물결(Ripple)치듯 올라가는 형태로 리플 캐리 가산기라는 명칭을 가지고 있다. 구조가 단순하지만 이전 가산기의 연산결과를 기다려야하는 지연시간이 존재한다(이를 리플 지연이라 부른다.) 이를 예방하고자 자리올림을 미리 예측하는 가산기(이러면 리플지연은 없어진다)도 존재한다.
부호기와 복호기 – 부호기(Encoder)
사용자는 임의의 선택을 할 때 이를 적절한 이진수로 변환하는 회로를 의미한다. 보통 부호화(Encoding)을 한다는 것은 데이터를 코드화 하는 것을 의미하는데, 임의의 선택선(I0~In)을 이진화한다는 점에서 부호기라고 칭할 수 있다.
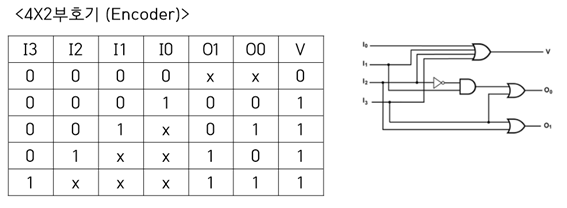
위에서 보다시피 입력 I0~I3까지 중 한가지를 코드화 한다. V는 입력이 존재하는 가를 표현하는 출력선으로 I0~I3모두가 선택되지 않았을 때 만 0이 출력된다.(모두 OR Gate) 이후 In은 n을 이진수로 출력한 결과가 O0와 O1에 비트로써 출력된다. 4개의 입력선택선과 2개의 이진비트출력을 가지기에 4 x 2라는 수식어가 앞에 붙어있다.
부호기와 복호기 – 복호기(Decoder)
조합논리회로에서 부호기와 반대로 복호기는 주어진 2진 입력으로부터 적절한 출력선 1개에 해당하는 번호에만 1을 출력하는 회로이다.
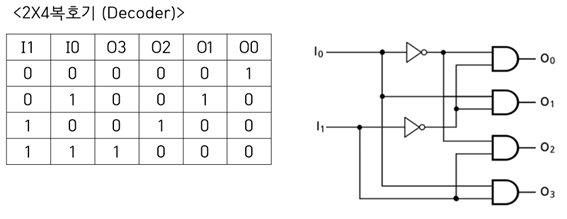
멀티플렉서(MUX)와 디멀티플렉서(DeMUX) - MUX
멀티플렉서는 데이터 선택기로 불리는데 복수개의 입력신호가 존재할 때 특정 조건(S0~S1)에 의해 한 개의 입력신호를 선택할 때 사용된다.
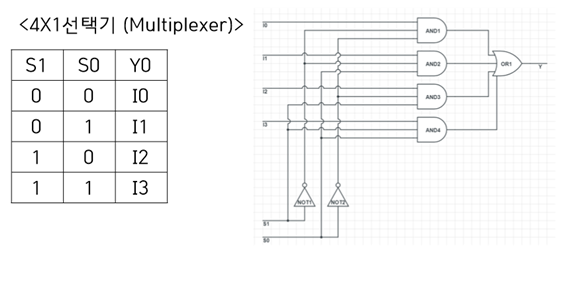
위에 회로진리표를 보듯이 4개의 입력선(I0~I3)중에서 S0와 S1조건에 따라 하나의 출력을 Y로 보내고 있다. 위에회로에서는 4개의 선 중 하나를 선택하기 때문에 4X1이고 역시 유연하게 변경가능하다.
멀티플렉서(MUX)와 디멀티플렉서(DeMUX) - DeMUX
반면에 DeMUX는 n개의 입력중 선택하면 MUX와 반대로 1개의 입력석은 조건에 따라 N개의 출력선에 선택하여 출력하는 회로이다. 데이터 분배기(Distributer)라고 부른다.
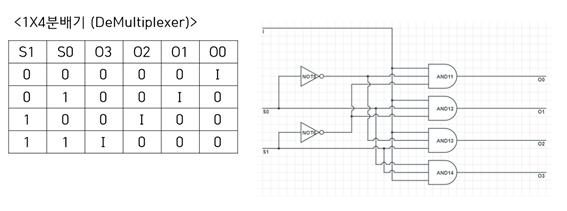
위에서 입력선 I는 조건 S0와 S1의 비트에 따라서 O0~O3 중 적절한 곳에 출력된다.
추가로 시험범위로 명시되어있지는 않지만 감산기라는 조합논리회로도 존재한다. 뺼셈이 기본적으로는 존재하지 않는 디지털 세상에서 보수체계를 통한 가산기로 수행되는 계산인데, 자세한 것은 위키백과를 참고하기를 바란다.
감산기 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전.
ko.wikipedia.org
정리
이번시간에는 기본적인 논리게이트의 표기법과 조합논리회로(가산기 / 선택기 / 분배기 / 부호기 / 복호기)의 구조를 알아보았다.
다음시간에는
오류수정코드인 패리티 비트와 해밍코드를 알아보도록 하겠다.
'자격 > 임베디드기사' 카테고리의 다른 글
| [임베디드기사] [필기] 순서논리회로(래치 & 플립플롭) (0) | 2023.08.14 |
|---|---|
| [임베디드기사] [필기] 2진 오류검출과 수정(패리티 비트 / 해밍코드) (0) | 2023.08.14 |
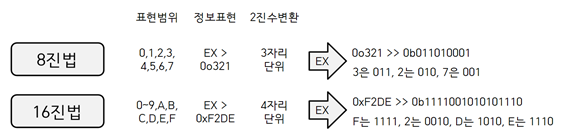
| [임베디드기사] [필기] 수의표현(2진수 / 8진수 / 16진수 / 10진수) (0) | 2023.08.13 |
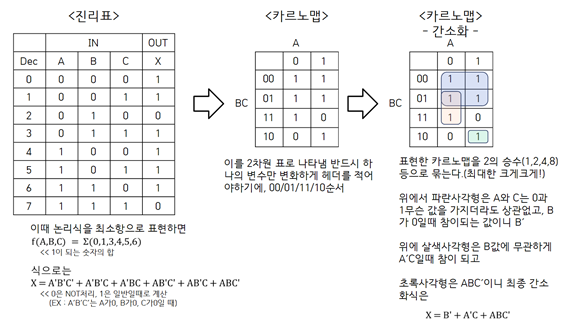
| [임베디드기사] [필기] 논리식의 간소화 (0) | 2023.08.13 |
| [임베디드기사] [필기] 불 대수(Boolean Algebra) (0) | 2023.08.12 |